Unresolved FEM-DEM model
for heated immersed granular flows
M.Henry, S.Dorbolo, J.Lambrechts, V.Legat


www.migflow.be
A brief history of granular rheology
A brief history of granular rheology
A brief history of granular rheology
A brief history of granular rheology
A brief history of granular rheology
Unresolved FEM-DEM model
- Solid phase
- Discrete element
- Lagrangian representation
- Insight in contacts physics
- Fluid phase
- Continuous medium
- Eulerian representation
- Computational convenience
- Fluid-grains interaction
- Empirical momentum transfer
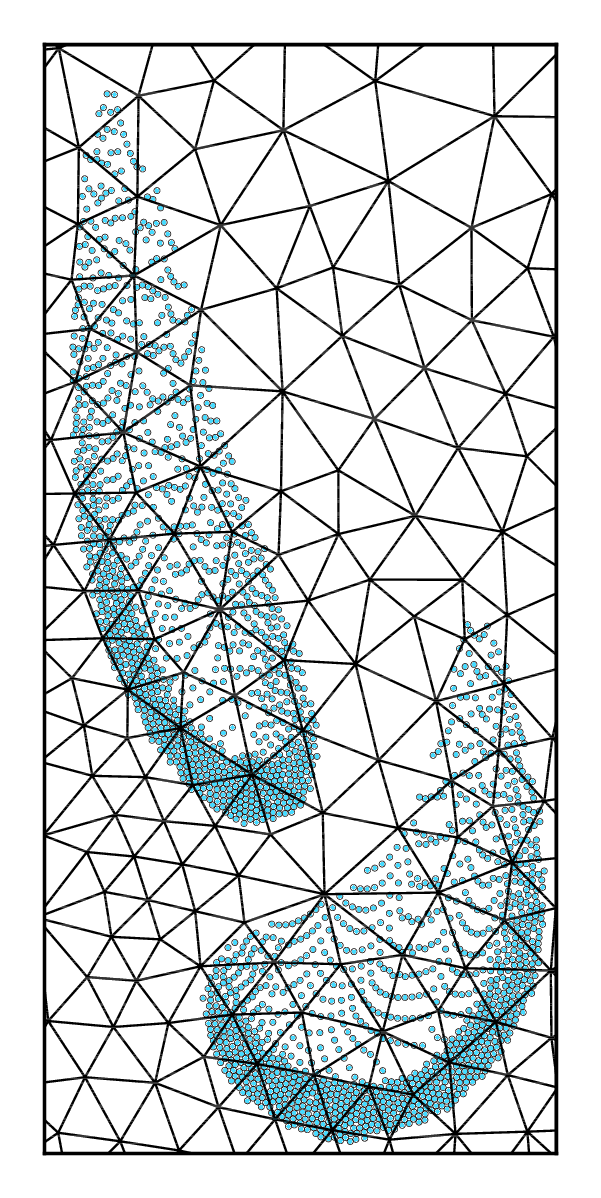
Non-smooth contact dynamics for dense regime
- Contact dynamics
- \[ \boldsymbol{M} \left(\boldsymbol{v}^+ - \boldsymbol{v}^-\right) = \boldsymbol{p} \]
- Signorini constraint
- \[ \left(\boldsymbol{v}^+ \cdot \boldsymbol{n}\right) \left(\boldsymbol{p} \cdot \boldsymbol{n} \right) = 0 \]
- Coulomb's friction law
- \[ \lVert \boldsymbol{p} - (\boldsymbol{p} \cdot \boldsymbol{n}) \boldsymbol{n} \rVert \leq \mu \left\vert \boldsymbol{p} \cdot \boldsymbol{n}\right\vert \]
Non-smooth contact dynamics for dense regime

- Contact dynamics
- \[ \boldsymbol{M} \left(\boldsymbol{v}^+ - \boldsymbol{v}^-\right) = \boldsymbol{p} \]
- Signorini constraint
- \[ \left(\boldsymbol{v}^+ \cdot \boldsymbol{n}\right) \left(\boldsymbol{p} \cdot \boldsymbol{n} \right) = 0 \]
- Coulomb's friction law
- \[ \lVert \boldsymbol{p} - (\boldsymbol{p} \cdot \boldsymbol{n}) \boldsymbol{n} \rVert \leq \mu \left\vert \boldsymbol{p} \cdot \boldsymbol{n}\right\vert \]
Volume averaged equations are solved
- Mass conservation
- \[ \frac{\partial \color{red}{\epsilon}}{\partial t} + \boldsymbol{\nabla} \cdot \left( \color{red}{\epsilon} \boldsymbol{u} \right) = 0 \]
- Momentum conservation
- \[ \color{red}{\epsilon} \frac{\text{D}\boldsymbol{u}}{\text{d}t} = -\color{red}{\epsilon} \boldsymbol{\nabla} p + \frac{1}{\text{Re}} \boldsymbol{\nabla} \cdot \left[ 2 \color{red}{\epsilon} \boldsymbol{d} (\boldsymbol{u}) \right] + \color{red}{\epsilon} \frac{1}{\text{Fr}^2} \boldsymbol{e_g} + \color{red}{\boldsymbol{f}} \]
- Energy conservation
- \[ \color{red}{\epsilon} \frac{\text{D}T}{\text{d}t} = \frac{1}{\text{Pr}\ \text{Re}} \boldsymbol{\nabla} \cdot \left[ \color{red}{\epsilon} \boldsymbol{\nabla} T \right] + \color{red}{q} \]
Both representations are coupled
- Particle conservation laws
- \[ \begin{aligned} m_i\frac{\text{d}\boldsymbol{v}_i}{\text{d}t} &= \boldsymbol{F}_e + \boldsymbol{F}_c\\ m_i c_{i} \frac{\text{d}T_i}{\text{d}t} &= Q_e + Q_c \end{aligned} \]
- External fluxes
- \[ \begin{aligned} \boldsymbol{F}_e &= \phantom{-} V_i \left(\rho_i\boldsymbol{g} - \boldsymbol{\nabla} p - \boldsymbol{f}_i\right)\\ Q_e &= -V_i q_i \end{aligned} \]
- From local to global scale
- \[ \begin{aligned} \boldsymbol{f} = \sum_{i\in \mathcal{P}} \boldsymbol{F}_i \delta|_{\boldsymbol{x}_i}, \\ q = \sum_{i\in \mathcal{P}} Q_i \delta|_{\boldsymbol{x}_i}, \end{aligned} \]
Heat transfer is similar to
momentum transfer along a sphere
- Drag force & forced convection :
- \[ \begin{aligned} F_d &\propto \text{C}_D \\ Q_e &\propto \text{Nu} \end{aligned} \]
- Duan & Duan showed Reynolds analogy for a sphere
- \[ \begin{aligned} \text{Nu}_W &= 2 + 0.6 \text{Re}^{0.5} \text{Pr}^{2/5}, \quad \text{Whitaker} \\ \text{Nu}_D &= \frac{\text{C}_D}{12} \frac{1}{f(\text{Re})} \text{Re} \text{Pr}^{2/5}, \quad \text{Duan} \\ \end{aligned} \]
- where $f(\text{Re}) = 1 + \frac{0.11\ \text{Re}^{1.4}}{\text{Re}+500}$
Heat transfer is similar to
momentum transfer along a sphere
- Drag force & forced convection :
- \[ \begin{aligned} F_d &\propto \text{C}_D \\ Q_e &\propto \text{Nu} \end{aligned} \]
- Duan & Duan showed Reynolds analogy for a sphere
- \[ \begin{aligned} \text{Nu}_W &= 2 + 0.6 \text{Re}^{0.5} \text{Pr}^{2/5}, \quad \text{Whitaker} \\ \text{Nu}_D &= \frac{\text{C}_D}{12} \frac{1}{f(\text{Re})} \text{Re} \text{Pr}^{2/5}, \quad \text{Duan} \\ \end{aligned} \]
- where $f(\text{Re}) = 1 + \frac{0.11\ \text{Re}^{1.4}}{\text{Re}+500}$
What about a multi-particle system ?
- The voidage function extends drag for a mixture :
- \[ \text{C}_D = g(\epsilon) \text{C}_{D,0}(\epsilon \text{Re}) \]
- Voidage function associated to Dallavalle correlation :
- \[ \begin{aligned} &\text{C}_{D,0} = \left(0.63 + \frac{4.8}{\left(\epsilon \text{Re}\right)^{0.5}}\right)^{2} \\ &g(\epsilon) = \epsilon^{-1.8} \end{aligned} \]
- Can we do the same for the Nusselt number ?
-
\[ \text{Nu} = g(\epsilon) \text{Nu}_{0}(\epsilon \text{Re})\]
What about a multi-particle system ?
- The voidage function extends drag for a mixture :
- \[ \text{C}_D = g(\epsilon) \text{C}_{D,0}(\epsilon \text{Re}) \]
- Voidage function associated to Dallavalle correlation :
- \[ \begin{aligned} &\text{C}_{D,0} = \left(0.63 + \frac{4.8}{\left(\epsilon \text{Re}\right)^{0.5}}\right)^{2} \\ &g(\epsilon) = \epsilon^{1.8} \end{aligned} \]
- Can we do the same for the Nusselt number ?
-
\[ \text{Nu} = g(\epsilon) \text{Nu}_{0}(\epsilon \text{Re}) \]
Reynolds analogy is valid for a packed bed
Let's consider a fluidification process
Let's consider a fluidification process
A bidimensional simulation
Particle temperature decrease at the nozzle
Bubble rises preferentially towards the domain center
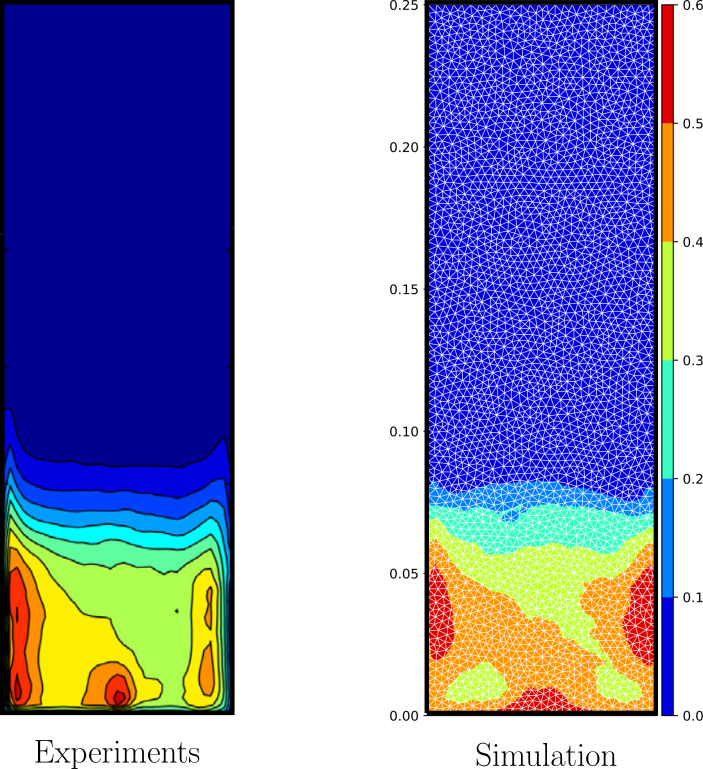
Proper correlations leads to quantitative results
Next perspectives :
towards phase change
- Water droplet digging
- Phase change
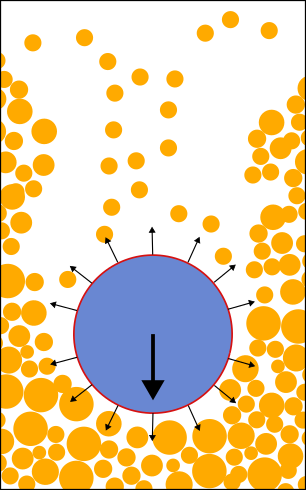
Next perspectives :
towards a semi-resolved model
- Polydisperse granular flows
- Accuracy
- Converging scheme
