Multi-scale model
for immersed granular flows

M.Henry, N.Coppin, S.Yans
J.Lambrechts, V.Legat

Immersed granular flows ?

• Geophysical flows : magma
• Civil engineering : concrete
• Pharmaceutical industries : drug powder
• Cooking : flour with water
• ...

Solid particles within a fluid

Multi-scale FEM-DEM model

• Solid phase
• Discrete element
• Lagrangian representation
• Insight in contacts physics
• Fluid phase
• Continuous medium
• Eulerian representation
• Computational convenience
• Fluid-grains interaction
• Empirical momentum transfer

MigFlow is a open-source software which supports ...

• Dry granular flow
• Semi-dilute regime
• Dense regime
• Free-surface flow (ALE, mesh adaptation)
• Free-surface with large deformation (PFEM)
• ...

MigFlow is a open-source software which supports ...

• Dry granular flow
• Semi-dilute regime
• Dense regime
• Free-surface flow (ALE, mesh adaptation)
• Free-surface with large deformation (PFEM)
• ...

MigFlow is a open-source software which supports ...

• Dry granular flow
• Semi-dilute regime
• Dense regime
• Two-phase flow
• Free-surface with large deformation (PFEM)
• ...

MigFlow is a open-source software which supports ...

• Dry granular flow
• Semi-dilute regime
• Dense regime
• Two-phase flow
• Free-surface with large deformation (PFEM)
• ...

MigFlow is a open-source software which supports ...

• Dry granular flow
• Semi-dilute regime
• Dense regime
• Two-phase flow
• Free-surface with large deformation (PFEM)
• ...

Non-smooth contact dynamics
to solve collision

• Contact dynamics
• \[ \boldsymbol{M} \left(\boldsymbol{v}^+ - \boldsymbol{v}^-\right) = \boldsymbol{p} \]
• Signorini constraint
• \[ \left(\boldsymbol{v}^+ \cdot \boldsymbol{n}\right) \left(\boldsymbol{p} \cdot \boldsymbol{n} \right) = 0 \]
• Coulomb's friction law
• \[ \lVert \boldsymbol{p} - (\boldsymbol{p} \cdot \boldsymbol{n}) \boldsymbol{n} \rVert \leq \mu \left\vert \boldsymbol{p} \cdot \boldsymbol{n}\right\vert \]

Non-smooth contact dynamics
to solve collision

• Contact dynamics
• \[ \boldsymbol{M} \left(\boldsymbol{v}^+ - \boldsymbol{v}^-\right) = \boldsymbol{p} \]
• Signorini constraint
• \[ \left(\boldsymbol{v}^+ \cdot \boldsymbol{n}\right) \left(\boldsymbol{p} \cdot \boldsymbol{n} \right) = 0 \]
• Coulomb's friction law
• \[ \lVert \boldsymbol{p} - (\boldsymbol{p} \cdot \boldsymbol{n}) \boldsymbol{n} \rVert \leq \mu \left\vert \boldsymbol{p} \cdot \boldsymbol{n}\right\vert \]

Let's have a look at another paradigm...

An explicit coupling is used,
overlapping drives the particle dynamics

GPU implementation is done by S. Yans
(more in a next seminar...)

Volume averaged equations are solved

• Mass conservation
• \[ \boldsymbol{\nabla} \cdot \left( \color{red}{\phi} \boldsymbol{u_s} \right) + \boldsymbol{\nabla} \cdot \left( \color{red}{\epsilon} \boldsymbol{u} \right) = 0 \]
• Momentum conservation
• \[ \color{red}{\epsilon} \frac{\text{D}\boldsymbol{u}}{\text{d}t} = -\color{red}{\epsilon} \boldsymbol{\nabla} p + \frac{1}{\text{Re}} \boldsymbol{\nabla} \cdot \left[ 2 \color{red}{\epsilon} \boldsymbol{d} (\boldsymbol{u}) \right] + \color{red}{\epsilon} \frac{1}{\text{Fr}^2} \boldsymbol{e_g} + \color{red}{\boldsymbol{f}} \]

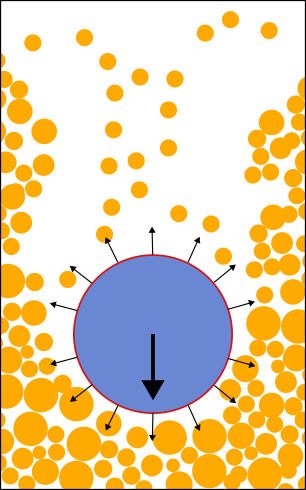
Drag force of a multi-particle system ?

• The drag force is characterised by the drag coefficient : \[ F_D \approx C_D \]
• The voidage function extends drag for a mixture :
• \[ \text{C}_D = g(\epsilon) \text{C}_{D,0}(\epsilon \text{Re}) \]
• Voidage function associated to Dallavalle correlation :
• \[ \begin{aligned} &\text{C}_{D,0} = \left(0.63 + \frac{4.8}{\left(\epsilon \text{Re}\right)^{0.5}}\right)^{2} \\ &g(\epsilon) = \epsilon^{-1.8} \end{aligned} \]

Discrete element method tracks particles

• Newton's second law
• \[ \begin{aligned} m_i\frac{\text{d}\boldsymbol{v}_i}{\text{d}t} &= \boldsymbol{F}_e + \boldsymbol{F}_c\\ \end{aligned} \]
• \[ \begin{aligned} \boldsymbol{F}_e &= V_i \left(\rho_i\boldsymbol{g} - \boldsymbol{\nabla} p - \boldsymbol{f}_i\right)\\ \end{aligned} \]

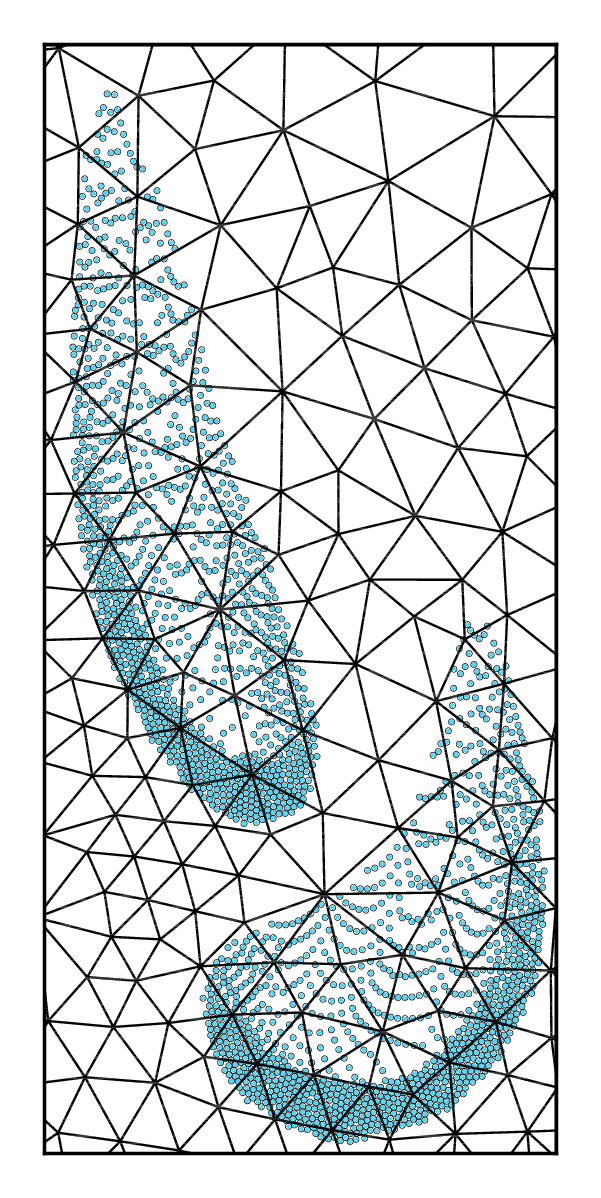
Mesh size is a computational cost parameter

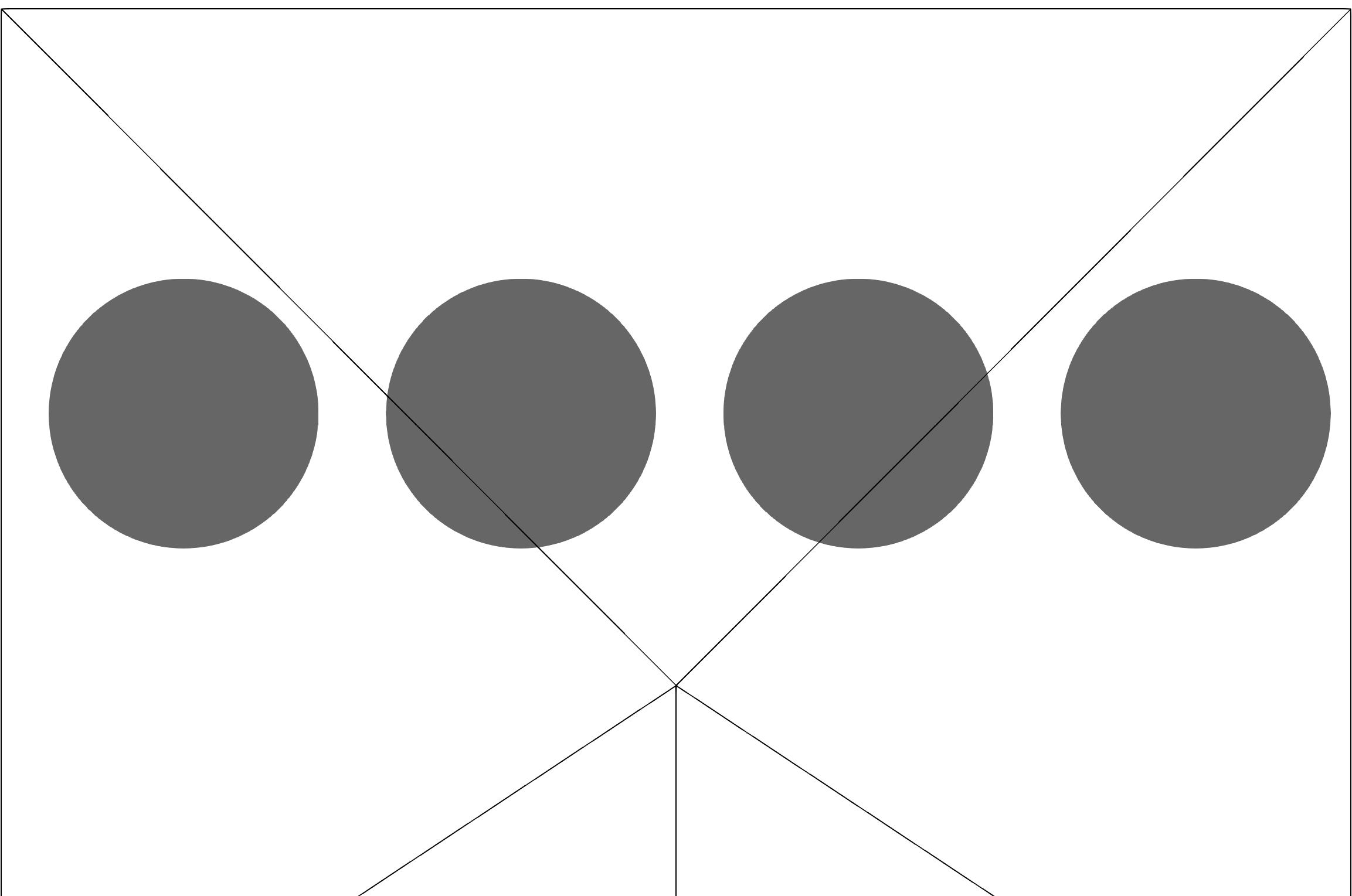
Unresolved
particle size < mesh size

resolved
particle size > mesh size

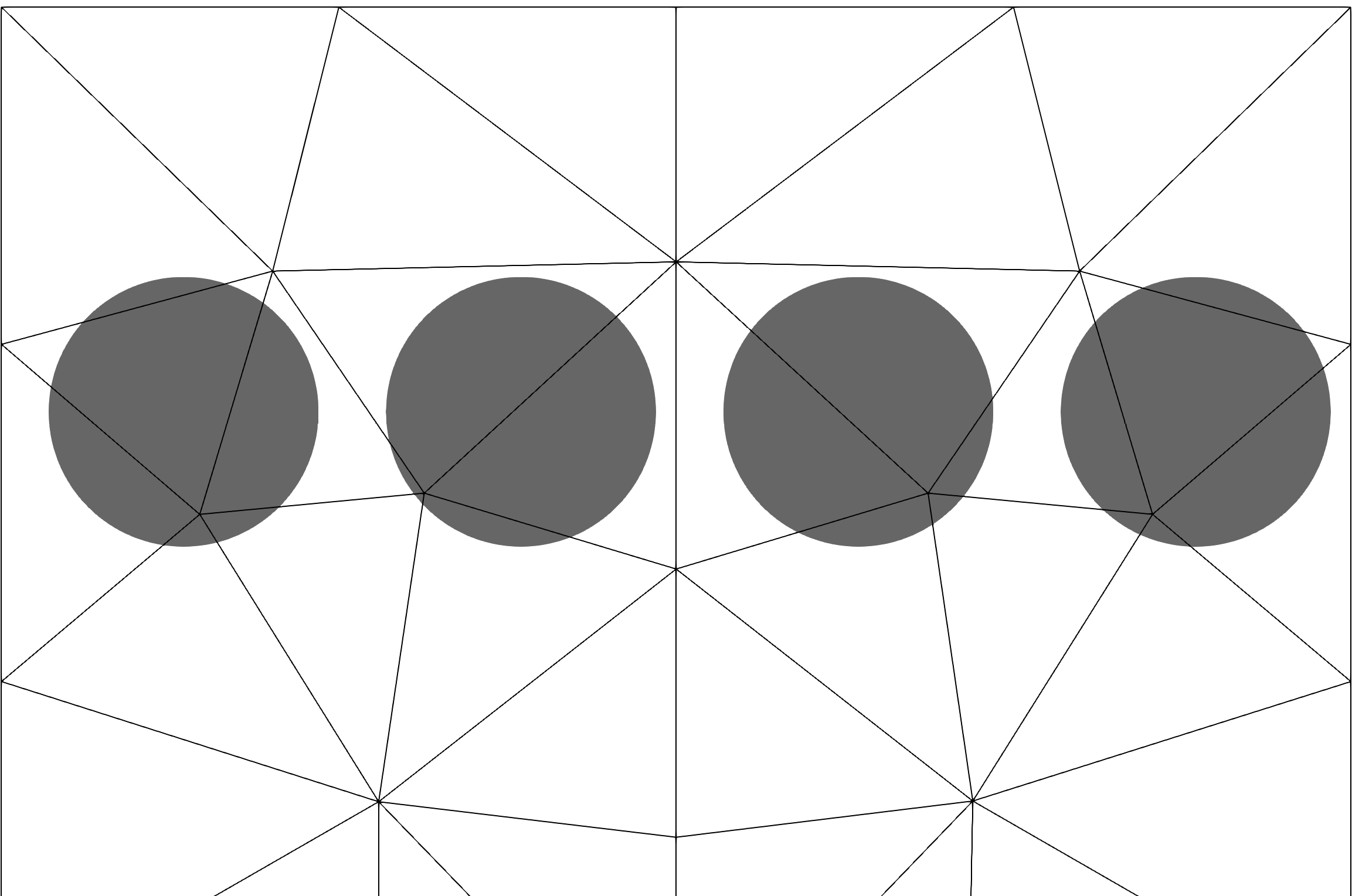
semi-resolved
particle size ~ mesh size

At resolved resolution,
how does it behave ?

• Mass conservation, $\epsilon \rightarrow 0$, $\phi \rightarrow 1$ : \[ \begin{aligned} &\boldsymbol{\nabla} \cdot \left( \color{red}{\phi} \boldsymbol{u_s} \right) &+ \boldsymbol{\nabla} \cdot \left( \color{red}{\epsilon} \boldsymbol{u} \right) &= 0 \\ &\boldsymbol{\nabla} \cdot \left(\phantom{\phi} \boldsymbol{u_s} \right) & &= 0 \end{aligned} \]


• Momentum conservation, $\epsilon \rightarrow 0$, $\phi \rightarrow 1$ : \[ \color{red}{\epsilon} \frac{\text{D}\boldsymbol{u}}{\text{d}t} = -\color{red}{\epsilon} \boldsymbol{\nabla} p + \frac{1}{\text{Re}} \boldsymbol{\nabla} \cdot \left[ 2 \color{red}{\epsilon} \boldsymbol{d} (\boldsymbol{u}) \right] + \color{red}{\epsilon} \frac{1}{\text{Fr}^2} \boldsymbol{e_g} + \color{red}{\boldsymbol{f}} \]
• It leads that : \[ \color{red}{\boldsymbol{f}} \triangleq \gamma \left( \boldsymbol{u} - \boldsymbol{u}^s\right) = 0 \]

At resolved resolution,
how does it behave ?

• Mass conservation, $\epsilon \rightarrow 0$, $\phi \rightarrow 1$ : \[ \begin{aligned} &\boldsymbol{\nabla} \cdot \left( \color{red}{\phi} \boldsymbol{u_s} \right) &+ \boldsymbol{\nabla} \cdot \left( \color{red}{\epsilon} \boldsymbol{u}^{\color{blue}{n+1}} \right) &= 0 \\ &\boldsymbol{\nabla} \cdot \left(\phantom{\phi} \boldsymbol{u_s} \right) & &= 0 \end{aligned} \]


• Momentum conservation, $\epsilon \rightarrow 0$, $\phi \rightarrow 1$ : \[ \color{red}{\epsilon} \frac{\text{D}\boldsymbol{u}}{\text{d}t} = -\color{red}{\epsilon} \boldsymbol{\nabla} p^{\color{blue}{n+1}} + \frac{1}{\text{Re}} \boldsymbol{\nabla} \cdot \left[ 2 \color{red}{\epsilon} \boldsymbol{d} (\boldsymbol{u}^{\color{blue}{n+1}}) \right] + \color{red}{\epsilon} \frac{1}{\text{Fr}^2} \boldsymbol{e_g} + \color{red}{\boldsymbol{f}} \]
• It leads that : \[ \color{red}{\boldsymbol{f}} \triangleq \gamma^{\color{blue}{n}} \left( \boldsymbol{u}^{\color{blue}{n+1}} - \boldsymbol{u}^s\right) = 0 \]

How to predict the particle velocity ?

• Newton's second law : \[ m\frac{\text{d}\boldsymbol{u_s}}{\text{d}t} = V_i \left(\rho_i\boldsymbol{g} - \boldsymbol{\nabla} p - \boldsymbol{f}_i\right) + \boldsymbol{F}_c \]
• Drag force : \[ \color{red}{\boldsymbol{f}} \triangleq \gamma^{\color{blue}{n}} \left( \boldsymbol{u}^{\color{blue}{n+1}} - \boldsymbol{u_s}\right) \]
• A semi-implicit scheme is used : \[ \begin{aligned} m\frac{\boldsymbol{u_s}^{\color{blue}{*}} - \boldsymbol{u_s}^{\color{blue}{n}}}{\Delta t} = &V_i \left(\rho_i\boldsymbol{g} - \boldsymbol{\nabla} p^{\color{blue}{n+1}} - \gamma^{\color{blue}{n}} \left( \boldsymbol{u}^{\color{blue}{n+1}} - \boldsymbol{u_s}^{\color{blue}{*}}\right) \right)\\ &+ \boldsymbol{F}_c^{\color{blue}{n}} \end{aligned} \]
• $\boldsymbol{u_s}^{\color{blue}{*}}$ provides the link with the pressure field

Granular Rayleigh-Taylor instabilities

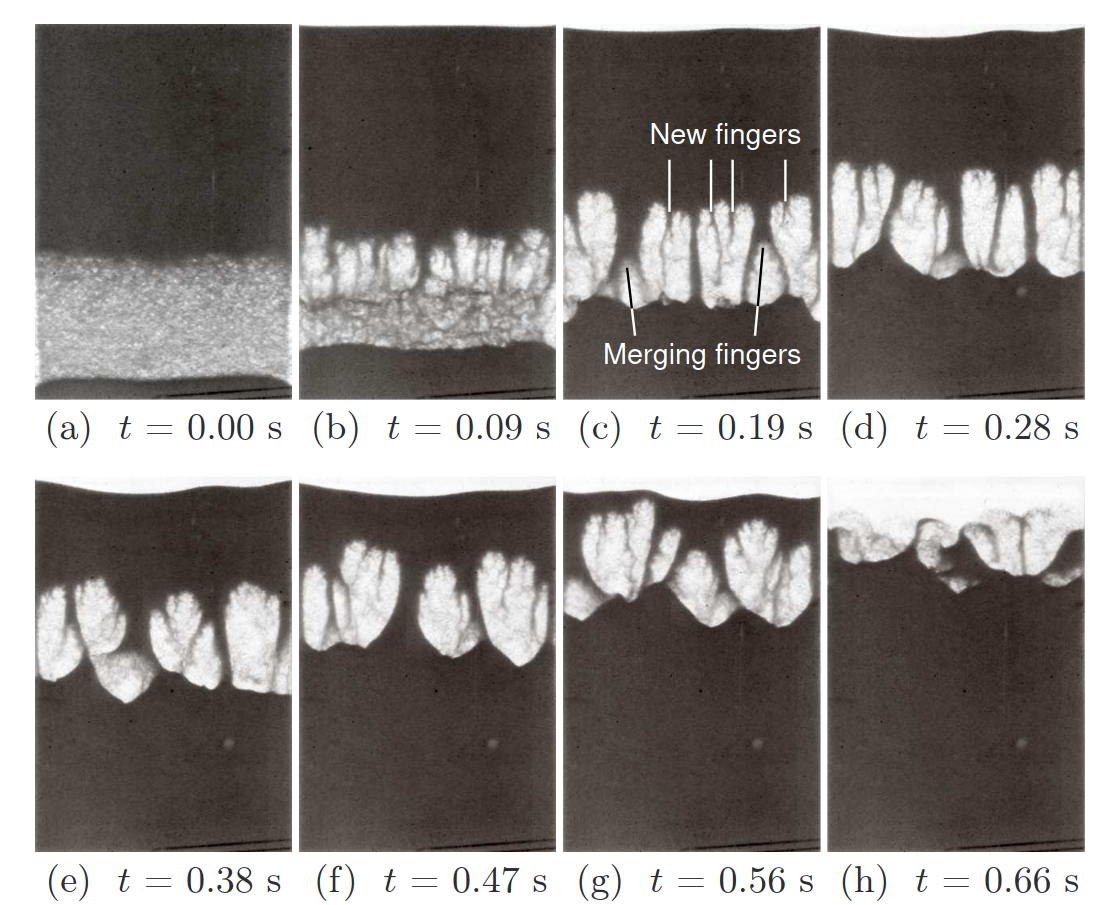
Granular Rayleigh-Taylor instabilities

A water droplet can dig into a granular bed

Granular bed is fluidized by Leidenfrost effect

The droplet digs up to 10 times its radius

Its depth depends on the granular temperature

An additional equation to solve

• Mass conservation
• \[ \frac{\partial \color{red}{\epsilon}}{\partial t} + \boldsymbol{\nabla} \cdot \left( \color{red}{\epsilon} \boldsymbol{u} \right) = 0 \]
• Momentum conservation
• \[ \color{red}{\epsilon} \frac{\text{D}\boldsymbol{u}}{\text{d}t} = -\color{red}{\epsilon} \boldsymbol{\nabla} p + \frac{1}{\text{Re}} \boldsymbol{\nabla} \cdot \left[ 2 \color{red}{\epsilon} \boldsymbol{d} (\boldsymbol{u}) \right] + \color{red}{\epsilon} \frac{1}{\text{Fr}^2} \boldsymbol{e_g} + \color{red}{\boldsymbol{f}} \]
• Energy conservation
• \[ \color{red}{\epsilon} \frac{\text{D}T}{\text{d}t} = \frac{1}{\text{Pr}\ \text{Re}} \boldsymbol{\nabla} \cdot \left[ \color{red}{\epsilon} \boldsymbol{\nabla} T \right] + \color{red}{q} \]

Reynolds analogy is valid for particles within air

Reynolds analogy is valid for particles within air

Let's investigate the droplet

The droplet levitates too quickly, any idea ?